If you are considering applying for Engineering at Oxbridge, you will need to have a solid understanding of Mathematics as it plays a significant role in the courses.
Mathematics is the cornerstone of Engineering. Without it, bridges would collapse under tension, lightbulbs might blow every time you flip a switch in your house, and your car brakes would only work some of the time.
But what areas of Mathematics do you need to know?
Mathematics at A-Level
If you are thinking of applying for Engineering at Oxbridge, Further Maths at A-Level is not a requirement, and you will not be disadvantaged by not taking it.
However, if your school or college does offer Further Maths, you are strongly encouraged to do so. Oxford and Cambridge acknowledge it is not an option available to everyone, which is why it is not essential to study Engineering.
It is worth noting; however, there is a high level of synergy between Maths, Further Maths and Physics. Any students who are taking this combination are encouraged to take a fourth A-Level to demonstrate both high achievement in Maths and the ability to cope with a demanding workload.
Worried about your Oxbridge chances? Our offer success rate for Engineering is 53%.
The Mathematics Subject Structure
The choice of a Mathematics A-Level course to follow and the choice of options or modules within that course is an important decision to make. That choice will be influenced by many factors, with the primary one being to go on to university courses in science subjects.
The assumed knowledge at the start of the first-year Mathematics course is set out below in the form of a syllabus based very closely on the national Core Syllabus in Mathematics, which was proposed in the early 1990s.
Algebra
One of the areas of Mathematics you will need to know to study Engineering at Oxbridge is algebra. Algebra covers the laws of indices (including negative and rational exponents);
- Addition
- Subtraction
- Multiplication
- Factorisation of polynomials
- Factor theorem
- The use of the modulus sign
- Solution of linear and quadratic inequalities and equations
- Solution of simultaneous linear equations
Engineers use linear algebra to design and analyse complex systems. Civil engineers use linear algebra to design and analyse load-bearing structures such as bridges. Mechanical engineers use linear algebra to design and analyse suspension systems, and electrical engineers use it to design and analyse electrical circuits.
Electrical, biomedical, and aerospace engineers use linear algebra to enhance x-rays, tomographs, and images from space.
Cartesian Geometry
Another area of Mathematics you will need to study Engineering at Oxbridge is Cartesian Geometry. The knowledge you will be expected to have is:
- Cartesian coordinates in two and three dimensions
- Distance between points
- Cartesian basis vectors i, j, k, and representation by vectors
- Equation of a straight line in the form y = mx + c
- Finding an equation of a linear graph
- Cartesian and parametric equations of curves.
Also known as analytical geometry, Cartesian Geometry is used in Physics and Engineering and plays a key part in aviation, rocketry, space science and spaceflight. Usually, the system is applied to manipulate equations for planes, straight lines, and circles, often in two and sometimes three dimensions.
Simply put, it is concerned with defining and representing geometric shapes numerically and extracting numerical information from shapes’ numerical definitions and representations.
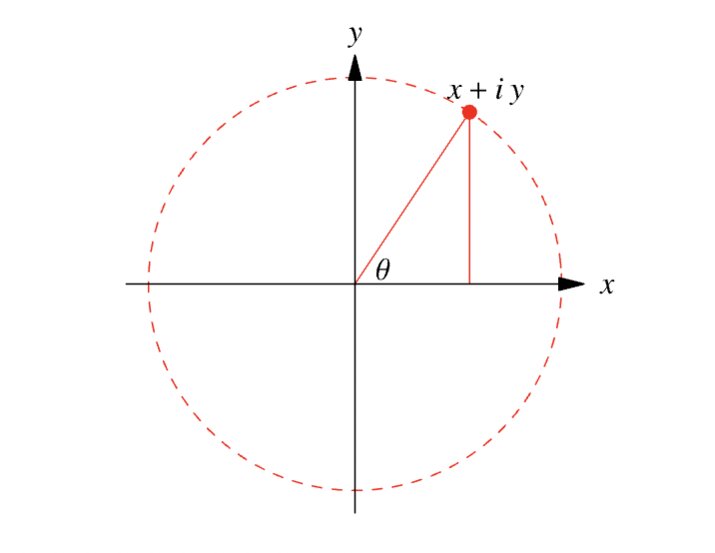
Complex Numbers
Complex numbers are another area of Mathematics you will be required to understand to study Engineering at Oxbridge.
The knowledge of complex numbers you are expected to have for Oxbridge Engineering is:
- The idea of complex numbers
- Real and imaginary parts, modulus, and argument
- Addition, subtraction, multiplication, and division of complex numbers
- The Argand diagram
Complex numbers are most commonly used in electrical engineering because Fourier transforms are used in understanding oscillations that occur both in alternating current and in signals modulated by electromagnetic waves.
Matrices
Matrices is another critical area of Mathematics that is essential to studying Engineering at Oxbridge.
This area focuses on:
- The representation of two simultaneous linear equations with a 2x2 matrix
- Addition and multiplication of 2x2 matrices
- Determinant and inverse of 2x2 matrices
Matrices can be solved physically related application and one applied in the study of electrical circuits, quantum mechanics and optics, with the help of matrices, calculation of battery power outputs, resistor conversion of electrical energy into another useful energy. These matrices play a role in calculation.
Functions
Engineers often make mathematical models of real-life systems to make predictions about how that system might behave. We can think of a function as a “processor” that takes in one (or more) input variables and produces an output variable.
You would be expected to have knowledge of:
- Graphical representations and their inverses
- Understanding domain, range, and composition
- Knowledge of the effect of simple scaling and shifting transformations of y = f(x) as represented by y = af(x), y = f(x) + a, y = f(x + a), y = f(ax)
Early preparation is key to a successful Oxbridge Engineering application.
Sequences and series
A strong understanding of sequence and series is fundamental to the study of discrete-time signals and systems. A discrete-time system response takes the form of a sequence, and the characteristics of these sequences and of the associated series dictate system properties such as causality, stability, memory, and finite vs infinite impulse response.
Additionally, sequence and series are the basis of discrete-time Fourier series and transforms, which provide the primary tool for frequency-domain signals and systems analysis.
Subsequently, the mathematical understanding you will be expected to have when studying at Oxbridge is as follows:
- Definition of sequences
- Recognition of periodicity, oscillation, convergence and divergence
- Arithmetic and geometric series
- Sum to infinity of a convergent geometric series; binomial expansion of (1 + x)^n
Trigonometry
Trigonometry is a branch of Mathematics that explores the relationships between the lengths of triangle sides and angles. Engineers routinely use trigonometric concepts to calculate angles. Civil and mechanical engineers use trigonometry to calculate torque and forces on objects, such as bridges.
The concepts you will need to know are:
- Radian measure
- The formulae s = rt and A = r2t/2, for length r and angle t. Sine, cosine, and tangent functions, their graphs, symmetries and periodicity
- Formulae for sin(A + B), sin(A - B), cos(A + B)
- Double angle formulae
Exponentials and logarithms
All types of engineers use natural and common logarithms. Chemical engineers use them to measure radioactive decay and pH solutions, which are measured on a logarithmic scale. Exponential equations and logarithms are used to measure earthquakes and to predict how fast your bank account might grow. Biomedical engineers use them to measure cell decay and growth and measure light intensity for bone mineral density measurements.
When studying Engineering at Oxbridge, you will be expected to know the following:
- Definition and properties of ex and ln x including their graphs
- Laws of logarithms
- Exponential growth and decay
- The solution of equations of the form ax = b
Differentiation and Integration
Differentiation and integration are particularly useful in engineering and are generally used for optimisation and summation. Many examples of this use of Mathematics are found in mechanical engineering, such as computing the surface area of complex objects to determine frictional forces, designing a pump according to flow rate and head, and calculating the power provided by a battery system.
Other examples can also be found in aerospace engineering. Thrust overtime calculated using the ideal rocket equation, for example. Analysis of rockets that function in stages also requires calculus, as does gravitational modelling over time and space. Almost all physics models, especially those of astronomy and complex systems, use some form of differentiation and integration.
The concepts of differentiation you are expected to know for Oxbridge Engineering are:
- The concepts of derivative as gradient
- Differentiation and its relation to the idea of a limit
- Algebraic differentiation of polynomials
- Differentiation of ex, ln x, sin x, cos x and tan x
- Application of differentiation to gradients, maxima and minima and stationary points
- Increasing and decreasing functions
- Rates of change
- Differentiation of functions using sums, differences, products, quotients and composition
- Differentiation of inverse functions
- Formation of simple differential equations
As for integration, you will need to know:
- The concept of integration
- Evaluation of area under a curve
- Integration as the inverse of differentiation
- Integration of xn, ex, 1/x, sin x, cos x
- Evaluation of definite integrals with fixed limits
- Simple cases of integration by substitution and by parts
- Solution of simple differential equations by either analytic or numerical means
The Application of mathematics
The final area of Mathematics you will need to understand to study Engineering at Oxbridge is the application of Mathematics.
For this, you will be required to have:
- An understanding of the process of mathematical modelling with reference to one or more application areas
- Abstraction from a real-world situation to a mathematical description
- The selection and use of a simple mathematical model to describe a real-world phenomenon
- Approximation, simplification, and solution
- Interpretation and communication of mathematical results and their implications in real-world terms
- Progressive refinement of mathematical models.
Conclusion
If you go into an Oxbridge Engineering degree with this pre-existing knowledge behind your back, you will be in a very strong position.
Preparatory problems are provided along with detailed references to enable self-study. Those who have missed some topics are advised to use these resources to make up for this deficit.
Of course, knowing which areas will benefit you and having a thorough grounding in them will be of an obvious advantage.
Our expert tutors will help you achieve the strongest possible Mathematics score on the ESAT and the PAT.